Anda sudah berada diblogger saya, semoga apa yang terpost diblog ini bermanfaat bagi anda sekalian. Ketika anda berada dan membaca artikel yang dipost, saya harap anda bisa memberikan komentar, kritikan, dan saran. Agar supaya yang dipost oleh saya menjadi lebih baik danbermanfaat bagi saudara yang telah membuka blog saya ini. Terima kasih.
Hidup Selalu Dalam Sebuah Bayangan
Materi Pemograman Dasar UNIB
MATERI KULIAH PEMOGRAMAN DASAR
Disusun Oleh : Sunardi M.M
FAKULTAS SAINS DAN TEKNOLOGI PRODI TEKNOLOGI INFORMASI
UNIVERSITAS IBRAHIMY SUKOREJO SITUBONDO
2018
DASAR LOGIKA DAN ALGORITMA
PENGERTIAN DASAR LOGIKA
Diperkenalkan pertama kali oleh Aristoteles (384-322 SM)
ALGORITMA Diperkenalkan Oleh Ahli Matematika : Abu Ja’far Muhammad Ibnu Musa Al Khawarizmi. Seorang ilmuan Persia yang menulis kitab al jabr w’al muqabala (rules of restoration and reduction) sekitar tahun 825 M
Definisi Logika
1. penalaran atau bentuk pemikiran.
2. ilmu yang memberikan prinsip-prinsip yang harus diikuti agar dapat berfikir valid menurut aturan yang berlaku.
Definisi Algoritma
1. Langkah – langkah yang dilakukan agar solusi masalah dapat diperoleh.
2. Suatu prosedur yang merupakan urutan langkah-langkah yg berintegrasi.
3. Suatu m etode khusus yang digunakan untuk menyelesaikan suatu masalah yang nyata.(Webster Dictionary)
TAHAP PENYELESAIAN MASALAH
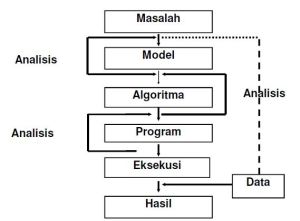 Kriteria Pemilihan Algoritma.
Kriteria Pemilihan Algoritma.1. Ada Output,
2. Efektifitas dan Efesiensi,
3. Jumlah Langkahnya Berhingga,
4. Berakhir, ( SEMI ALGORITMA )
5. Terstruktur,
Suatu Algoritma yg terbaik (The Best) : “ Suatu algoritma harus menghasilkan output yg tepat guna (efektif) dlm waktu yg relatif singkat & penggunaan memori yg relatif sedikit (efesien) dgn langkah yg berhingga & prosedurnya berakhir baik dlm keadaan dip’oleh suatu solusi ataupun tdk ada solusinya. “
Contoh :
Sebuah prosedur ketika akan mengirim kan surat kepada teman:
1. Tulis surat pada secarik kertas surat
2. Ambil sampul surat atau amplop
3. Masukkan surat ke dalam amplop
4. Tutup amplop surat dengan lem perekat
5. Tulis alamat surat yg dituju, jika tdk ingat, lebih dahulu ambil buku alamat & cari alamat yg dituju, lalu tulis alamat tsb pd amplop surat.
6. Tempelkan perangko pada am plop surat
7. Bawa surat ke kantor pos utk diserahkan pd pegawai pos atau menuju ke bis surat untuk memasukkan surat ke dlm kotak/bis surat.
Sebuah prosedur untuk masalah menentukan akar kuadrat dari suatu bilangan Bulat Positif yg di Input :
Baca bilangan Bulat Positif yg diinput, sebut saja sebagai A
1. Dinyatakan Nilai B adalah 0
2. Hitung Nilai C yg berisikan Nilai B dikalikan Nilai B
3. Jika Nilai C sama dengan Nilai A, maka Nilai B adalah Akar dari Nilai A, lalu stop.
4. Jika tidak, maka Nilai B akan bertambah 1
5. Kembali ke langkah pada No. 3
TAHAPAN ANALISA ALGORITMA
1. Bagaimana merencanakan suatu algoritma.
2. Bagaimana menyatakan suatu algoritma
a. Dengan bahasa semu (pseudocode).
Contoh :
Untuk menghitung Luas Segi tiga :
1. Masukan Nilai Alas
2. Masukan Nilai Tinggi
3. Hitung Luas =( Alas * Tinggi ) / 2
4. Cetak Luas
b. Dengan diagram alur atau flowchart,
Contoh :
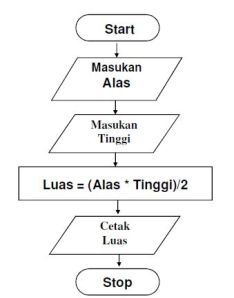 c. Dengan Statement program / penggalan
c. Dengan Statement program / penggalanProgram
Contoh (menggunakan C++):
cin >> Alas ; //untuk input data
cin >> Tinggi;
Luas = (Alas * Tinggi)/2 ; // proses
cout << Luas; //untuk output data
3. Bagaimana validitas suatu algoritma.
4. Bagaimana Menganalisa suatu Algoritma.
5. Bagaimana Menguji Program dari suatu Algoritma.
Tahap Proses uji Algoritma :
a. Fase Debugging
yaitu fase dari proses program eksekusi yang akan melakukan koreksi terhadap kesalahan.
b. Fase Profilling
yaitu fase yang akan bekerja jika program tersebut sudah benar (telah melewati fase debugging).
Analisis Suatu Algoritma
(Untuk melihat faktor efesiensi & efektifitas dari algoritma tersebut), Dapat dilakukan terhadap suatu algoritma dengan melihat pada :
a. Waktu Tempuh (Running Time) dr suatu Algortima.
Hal-hal yg dpt m empengaruhi drpd waktu tempuh adalah :
1. Banyaknya langkah.
2. Besar dan jenis input data.
3. Jenis Operasi.
4. Komputer dan kompilator
b. Jumlah Memori Yang Digunakan.
Sifat – Sifat Algoritma
• Banyaknya Langkah Instruksi Harus Berhingga,
• Langkah atau Instruksi harus Jelas,
• Proses harus Jelas dan mempunyai batasan,
• Input dan Output harus mempunyai Batasan,
• Efektifitas,
• Adanya Batasan Ruang Lingkup
x
Dampak Makanan Kaleng
KARYA ILMIAH SEDERHANA
POSITIF DAN NEGATIF MAKANAN KALENG
POSITIF DAN NEGATIF MAKANAN KALENG
Disusun Oleh : Taufiq Hidayatullah
FAKULTAS SAINS DAN TEKNOLOGI PRODI TEKNOLOGI INFORMASI
UNIVERSITAS IBRAHIMY SUKOREJO SITUBONDO
2018
2018
Positif dan Negatif Makanan Kaleng
BAB I
PENDAHULUAN
PENDAHULUAN
1. Latar Belakang
Makanan kaleng masuk ke dalam kategori makanan instan atau cepat saji (junk food). Menurut penelitian yang pernah dilakukan di Jepang, makanan kaleng mengandung zat kimia Stannum (Sn). Zat ini sebenarnya tidak berbahaya bila dikonsumsi sesuai kebutuhan. Namun, zat Sn akan berbahaya bila dikonsumi melebihi empat belas miligram per kilogram berat tubuh.
2. Rumusan Masalah
Bagaimana dampak makanan kaleng bagi kesehatan tubuh?
3. Tujuan Penelitian
Untuk mengetahui dampak positif dan negatif makanan kaleng.
BAB II
PEMBAHASAN
PEMBAHASAN
Dampak Makanan Kaleng Bagi Tubuh
Makanan kaleng merupakan salah satu jenis makanan cepat saji yang diminati. Makanan kaleng identik dengan hewan seperti ikan atau biasa disebut sarden. Namun, tak hanya sarden, makanan kaleng juga dapat berisi sayuran, buah, hingga minuman. Makanan kaleng tidak selalu berdampak buruk bagi tubuh. Ia juga memiliki keunggulan. Dampak positif dan negatif makanan kaleng, yaitu:
1. Dampak positif
a. Menghemat waktu penyajian
b. Kaleng menjaga makanan dari kontaminasi organisme penyebab penyakit
c. Makanan kaleng tidak kekurangan zat gizi
b. Kaleng menjaga makanan dari kontaminasi organisme penyebab penyakit
c. Makanan kaleng tidak kekurangan zat gizi
2. Dampak negatif
a. Membuat para Ibu malas memasak
b. Jika dikonsumsi berlebih dapat menyebabkan penyakit berbahaya seperti tekanan darah tinggi dan kolesterol
c. Jika dimasak dengan suhu tinggi, gizi di dalamnya akan berkurang bahkan hilang.
b. Jika dikonsumsi berlebih dapat menyebabkan penyakit berbahaya seperti tekanan darah tinggi dan kolesterol
c. Jika dimasak dengan suhu tinggi, gizi di dalamnya akan berkurang bahkan hilang.
BAB III
PENUTUP
PENUTUP
Kesimpulan
Kesimpulan yang dapat diambil yaitu makanan kaleng memiliki dampak positif dan negatif. Dampak negatif akan terjadi bila makanan kaleng yang dikonsumsi melampaui batas. Selain itu, cara masak juga memengaruhi baik buruknya makanan kaleng terhadap kesehatan tubuh. Disamping dampak tak menyenangkan yang ia miliki, makanan kaleng juga memberi dampak positif seperti yang telah dibahas.
Bahaya Pergaulan Bebas di Kalangan Remaja
KARYA ILMIAH SEDERHANA
BAHAYA PERGAULAN BEBAS DIKALANGAN REMAJA
BAHAYA PERGAULAN BEBAS DIKALANGAN REMAJA
Disusun oleh:
Taufiq Hidayatullah
FAKULTAS SAINS DAN TEKNOLOGI PRODI TEKNOLOGI INFORMASI
UNIVERSITAS IBRAHIMY SUKOREJO SITUBONDO
2018
Bahaya Pergaulan Bebas di Kalangan Remaja
BAB I
PENDAHULUAN
PENDAHULUAN
1. Latar Belakang
Usia remaja merupakan usia yang rawan khususnya dalam pergaulan. Kemajuan teknologi juga memicu luasnya pergaulan. Pada masa kini, pergaulan bebas menjadi bahaya utama yang dihadapi kalangan remaja. Tak hanya itu, pergaulan bebas juga menimbulkan kekhawatiran para orang tua. Usia remaja yang labil memang sangat mudah “dibodohi” pergaulan.
2. Rumusan Masalah
Bagaimana bahaya pergaulan bebas bagi para remaja?
3. Tujuan penelitian
Mengetahui bahaya apa saja yang mengancam sebagai akibat dari pergaulan bebas.
BAB II
PEMBAHASAN
PEMBAHASAN
Bahaya Pergaulan Bebas
Pergaulan tak selamanya memberikan efek yang baik. Pergaulan yang buruk atau biasa disebut pergaulan bebas ialah salah satu contoh pergaulan dengan efek buruk. Dampak negatif dari pergaulan bebas, yaitu:
a. Kerusakan moral anak
Pergaulan bebas merupakan salah satu penyebab rusaknya moral anak bangsa. Mereka merasa bebas tanpa diperhatikan oleh orang tua. Sehingga mereka kehilangan akhlak baik yang seharusnya dimiliki. Berbagai hal negatif dapat mereka lakukan untuk memenuhi rasa bahagia. Pergaulan bebas menyebabkan anak kehilangan sikap sopan dan hanya mengikuti zaman.
b. Penggunaan narkotika dan minuman keras
Seperti yang telah banyak diberitakan, para remaja kini banyak yang “terciduk” sedang berpesta miras maupun narkoba. Bahkan, tak hanya remaja, anak-anak usia dini juga telah menghisap rokok. Obat-obat terlarang ini mudah ditemukan bila seseorang telah masuk ke zona pergaulan bebas. Hal ini dikarenakan minuman keras dan narkotika dijual bebas dimana pun.
c. Kecelakaan sebelum menikah
Dampak negatif pergaulan bebas yang berdampak besar bagi diri sendiri maupun keluarga yaitu hamil duluan. Kurangnya sex education untuk remaja menjadi sebab utama. Kecelakaan sebelum menikah bahkan telah terjadi pada anak usia Sekolah Dasar (SD). Mereka tidak mengetahui apa yang mereka lakukan dan juga dampak setelah mereka melakukan hal tersebut.
BAB III
PENUTUP
PENUTUP
Kesimpulan
Pergaulan pada masa kini telah memasuki zona berbahaya. Dampak negatif dari pergaulan bebas telah memakan banyak mangsa. Mulai dari kerusakan moral dan penggunaan obat terlarang serta kecelakaan sebelum nikah. Pergaulan bebas yang terjadi di kalangan remaja dapat dikurangi melalui perantara utama yaitu orang tua. Orang tua harus memberikan edukasi dan pengawasan yang cukup kepada anak.
Pencemaran Dalam Lingkungan Hidup
KARYA ILMIAH SEDERHANA
TENTANG PENCEMARAN LINGKUNGAN
TENTANG PENCEMARAN LINGKUNGAN
Disusun oleh:
Taufiq Hidayatullah
FAKULTAS SAINS DAN TEKNOLOGI PRODI TEKNOLOGI INFORMASI
UNIVERSITAS IBRAHIMY SUKOREJO SITUBONDO
2018
Pencemaran Dalam Lingkungan Hidup
BAB I
PENDAHULUAN
PENDAHULUAN
1. Latar Belakang
Lingkungan merupakan kesatuan antara abiotik dan biotik. Abiotik adalah kumpulan-kumpulan benda mati. Sedangkan biotik adalah kumpulan benda hidup. Di dalam komponen abiotik yaitu udara, air, cahaya matahari, tanah, suhu dan lain sebagainya. Komponen biotik mencakup dekomposer atau pengurai, konsumen, dan produsen. Kedua komponen ini sangat erat berkaitan (tak dapat dipisahkan).
Lingkungan hidup diartikan secara beragam. Menurut Kamus Ekologi, lingkungan hidup disebut juga environment. Environment ialah kesatuan antara makhluk hidup (biotik) dan non-hidup (abiotik) yang ada di bumi. Sedangkan, menurut Undang-Undang No. 32 Tahun 2009, lingkungan hidup adalah kesatuan ruang seluruh benda. Baik makhluk hidup termasuk manusia, keadaan hingga perilaku manusia.
Secara keseluruhan dapat disimpulkan bahwa lingkungan hidup adalah gabungan antara semua makhluk hidup dan faktor serta komponen sekelilingnya. Makhluk hidup yang ada di bumi merupakan salah satu faktor keberhasilan lingkungan hidup. Makhluk hidup yang dikhususkan yaitu manusia. Manusia adalah makhluk berakal yang diciptakan Tuhan dengan sempurna dalam keadaan yang utuh pula.
Oleh sebab itu, kegagalan lingkungan hidup seperti pencemaran yang terjadi dapat dikatakan ulah manusia. Tingkah laku manusia pada masa kini sudah melebihi batas wajar. Salah satunya yaitu membuang sampah sembarangan. Banyak tempat yang seharusnya bersih dari sampah justru tertimbun sampah. Tempat yang seharusnya rindang dan asri, berubah menjadi tempat yang panas dan gersang.
2. Rumusan Masalah
a. Apa saja jenis pencemaran bagaimana penjelasannya?
3. Tujuan Penelitian
Untuk mengetahui jenis pencemaran lingkungan hidup.
BAB II
PEMBAHASAN
PEMBAHASAN
A. Jenis Pencemaran
1. Pencemaran Udara
Pencemaran udara tak selalu disebabkan oleh ulah manusia. Pencemaran udara dapat pula disebabkan oleh kejadian alam contohnya gunung meletus. Hasil dari letusan gunung berapi membawa partikel-partikel logam yang berbahaya. Namun, penyebab utama pencemaran udara di Indonesia terjadi akibat polusi kendaraan bermotor roda dua, tiga maupun empat.
Pencemaran udara disebabkan beberapa hal berikut, yaitu:
a. Asap Rokok
Seperti yang telah diketahui, sebagian besar orang-orang terkaya yang ada di Indonesia ialah bos besar perusahaan rokok. Oleh sebab itu, tak heran bila asap rokok menjadi penyumbang pencemaran udara yang terbesar. Kandungan-kandungan berbahaya ada di dalam rokok seperti tar dan nikotin. Maka asap yang ditimbulkan berbahaya pula.
b. Ozon (O3)
Sudah menjadi rahasia publik bila lapisan ozon mulai menipis. Lapisan penghalang buruknya sinar matahari ini justru menjadi boomerang bagi bumi. Polutan ozon merupakan polutan yang paling berbahaya. Penangannya pun sangat sulit karena tak dapat dideteksi. Perlu untuk diketahui, polutan ozon menyebabkan kerusakan paru-paru.
c. Karbonmonoksida (CO)
Gas CO juga merupakan salah satu polutan yang berbahaya. Gas ini dapat menimbulkan kematian jika seseorang menghirupnya dalam waktu yang lama. Contoh dari polutan gas CO yaitu ketika tidur di dalam mobil menggunakan AC. Gas-gas CO yang dihasilkan kendaraan bermotor di luar dapat masuk ke dalam. Gas itulah yang mematikan.
2. Pencemaran Air
Air yang bersih yaitu air yang tidak berbau dan tidak berwarna. Sehingga bila diemui air yang berbau, berwarna dan terdapat biota yang mati di dalamnya, air itu terindikasi telah tercemar. Pencemaran pada air dapat disebabkan oleh hal-hal berikut:
a. Limbah pabrik, nuklir dan industri
Limbah pabrik, nuklir dan industri mengandung zat-zat kimia berbahaya. Salah satu zat itu ialah radioaktif. Pembuangan limbah secara sembarangan ke sungai sangat membahayakan. Karena zat berbahaya akan tercampur dengan air sungai. Hal itu mengancam keberadaan biota sungai dan lingkungan sekitar.
b. Bahan peledak untuk menangkap ikan
Penangkapan ikan menggunakan bahan peledak memang sudah dilarang. Namun, tetap saja ada oknum “nakal” yang menggunakannya. Penangkapan dengan bahan peledak dinilai efektif. Tidak akan memakan waktu yang lama dan akan mendapat hasil tangkapan melimpah. Namun, hal ini adalah salah satu penyebab pencemaran air.
c. Pestisida
Limbah pertanian sebenarnya tidak membahayakan. Namun, penggunaan pestisida yang berlebih dan pupuk kimia itulah yang menyebabkan pencemaran air. Limbah pertanian yang di dalamnya terdapat pestisida berlebih dan pupuk kimia akan mengalir. Kemudian hal tersebut menimbulkan pencemaran pada air.
d. Sampah
Sampah menjadi masalah utama di zaman sekarang. Kesadaran manusia akan lingkungan nampaknya sudah sangat rendah. Sampah-sampah rumah tangga dibuang di sembarang tempat. Mulai dari lorong air kecil (selokan) hingga ke sungai sudah dipenuhi sampah. Padahal, sampah menjadi salah satu penyebab dari pencemaran air.
3. Pencemaran Tanah
Suatu tanah dikatakan sudah tercemar ketika tanah itu tak dapat lagi digunakan untuk kebutuhan manusia. Kebutuhan yang dimaksud seperti bercocok tanam. Selain itu, tanah yang gersang juga suatu ciri tanah sudah tercemar. Penyebab pencemaran tanah, yaitu:
a. Senyawa asam
b. Pestisida berlebih
c. Pupuk kimia
d. Limbah industri, pabrik dan nuklir
e. Limbah rumah tangga misalnya deterjen.
b. Pestisida berlebih
c. Pupuk kimia
d. Limbah industri, pabrik dan nuklir
e. Limbah rumah tangga misalnya deterjen.
BAB III
PENUTUP
PENUTUP
Kesimpulan
Pencemaran dibagi menjadi tiga yaitu pencemaran air, tanah dan udara. Setiap pencemaran memiliki ciri tertentu. Setiap pencemaran juga memiliki penyebab tertentu. Penyebab pencemaran satu dan lainnya tidak jauh beda. Contohnya penggunaan pestisida berlebih. Untuk itu, manusia sebagai makhluk berakal di bumi wajib mengurangi penggunaan bahan-bahan penyebab pencemaran dan menjaga lingkungan.
Link Blog Teman Kampus
Taufiq : https://taufiqtau.blogspot.com
Muzayyin : https://amuecangkreng.blogspot.com
Rizal : https://belengsabe.blogspot.com
Kholeq : https://Kholikmumfarisa.blogspot.com
Wahed : https://wahedgokil.blogspot.com
Fahmi : https://fahmi024.blogspot.com
Raysal : https://raysal4far.blogspot.com
Mahmudi : https://Mahmudisarjana.blogspot.com
Nasihin : https://nasihinajha.blogspot.com
Ramdhan :
https://Ramdhanpemrograman.blogspot.com
Abd hamid :
https://OgenkHamid01.blogspot.com
Hanafi :
https://pembururawit.blogspot.com
Faizin :
https://faizinvespa.blogspot.com
Bias pandu : https://beritabps.blogspot.com
Wariono : https://wariyonosukorejo.blogspot.com
Malik : zivanka.blogspot.com
Puisi Pribadi
“ IBU ”
“Ibu......
ibu
kasih sayang-mu yang begitu besar...
tanpa inginkan suatu imbalan
tiada yang mampu memberikan kasih dan sayang melebihi-mu...
dikala terbangunm-u...
engkau dengan sabar untuk menjaga-ku
bahkan dikala tidur-mu..
engkau tanpa mengeluh bangun karena tangisan-ku...
dengan tabahnya diri-mu menjaga-ku siang sampai malam
merawat-ku dengan seluruh jiwa dan raga-mu...
ibu...... ibu
engkau memberikan jasa yang begitu besar...
memberikan dukungan yang begitu tinggi...
memberikan motifasi bagi-ku dengan ratapan do’a-mu pada sang Ilahi..
dalam setiap do’a-mu...
engkau panjatkan kehidupan sempurna bagi-ku
sedang kehidupan yang kau jalani begitu berat dan penuh dengan segala rintangan
tapi...
engkau dengan sabarnya memberikan dukungan kepada-ku
ibu..... ibu
aku bersimpuh dihadapan-mu dengan segala terima kasihku pada-mu”
“
CAHAYA ”
“Dikala duduk termenung...
melihat langit yang di penuhi cahaya bintang-bintang...
menghayati diri akan kehidupan
untuk menatap suatu tujuan
mencari makna setiap insan
meresap pada relung harapan...
intuisi yang menciptakan sebuah perubahan...
yang akan menjadikan diri akan sebuah kemajuan...
maju dalam setiap gerak langkah...
menuju suatu tujuan yang diinginkan
menatap sebuah cahaya...
yang memberikan suatu penerangan akan perjalanan...
merespon akan setiap perbuatan
dalam menghadapi sebuah rintangan...
melihat grafik dalam diri...
melihat peningkatan dan kemajuan yang dicapai dalam diri...”
“ BANGKIT ”
“bangkit
itu susah...!!!
susah melihat orang lain susah,
senang melihat orang lain senang.
bangkit itu takut...!!!
takut korupsi.
takut makan yang bukan haknya.
bangkit itu mencuri...!!!
mencuri perhatian dunia dengan
prestasi.
bangkit itu marah...!!!
marah bila martabat bangsa di
lecehkan.
bangkit itu malu...!!!
malu jadi benalu,
malu karna minta melulu.
bangkit itu tidak ada...!!!
tidak ada kata menyerah,
tidak ada kata putus asa.
Bangkit itu
aku...!!!
untuk negara indonesia-ku.”.
“ INTONASI ”
“dunia penuh dengan sebuah
“kejutan”
kehidupan penuh dengan sebuah
“khayalan”
tindakan penuh dengan sebuah
“resiko”
pilihan penuh dengan sebuah
“kesalahan”
perasaan penuh dengan sebuah
“kebimbangan”
kenyataan penuh dengan sebuah yang
“menyakitkan”
fikiran penuh dengan sebuah
“kelupaan”
kejadian penuh dengan sebuah
“pelajaran”
intonasi kehidupan yang penuh
“keajaiban”
Perjelana yang tak akan pernah
“Berkesudahan.””
“ RENKARNASI ”
“di mana ada cahaya..
maka di situ pulalah ada
kegelapan..
di setiap ada kehidupan
maka akan berakhir dengan sebuah
kematian...
jika sudah terjadi rasa kasih sayang,
maka di situlah terbesit sebuah rasa
kebencian...
saat berharap tentang perdamaian,
maka akan ada pula sebuah
kehancuran...
renkarnasi sebuah kehidupan,
akan terbentuk sebuah kisah masa
depan...
ketika setiap insan menginginkan harapan,
maka juga akan terjadi sebuah
kebuntuan...
kasih sayang tak akan pernah
sirna,
dan kebencian pasti akan selalu ada
di sampingnya.
sebuah kisah akan terus
berjalan,
dan akan berakhir dengan sebuah
kematian.”
“ ILMU ”
“Ilmu ...
mencarimu dengan seluruh usaha-ku,
mencarimu dengan berpeluh keringat-ku...
ilmu...
kau begitu angkuh dalam cara-mu
kau begitu sombong dengan diri-mu
kau begitu pelit dengan sifat-mu
ku berusaha mencari-mu...
tapi...
dengan tak acuh-mu, kau ingin pergi meninggalkan-ku
aku yang sudah mati-matian agar mendapatkan-mu
tapi kau selalu ingin mendapakan perhatian dari-ku
ilmu...
angkuh-mu tertutup oleh perhatian-mu
sombong-mu tertutup oleh pemberian-mu
dan pelitmu tertutup oleh kasih dan sayang-mu...
ilmu...
begitu sulit ku menebakmu.”
Materi Kalkulus UNIB
MATERI KULIAH KALKULUS
Disusun oleh:
Selvia Nuer Agustin, S.Ars.
FAKULTAS SAINS DAN TEKNOLOGI PRODI TEKNOLOGI INFORMASI
UNIVERSITAS IBRAHIMY SUKOREJO SITUBONDO
2018
Rumus Integral Matematika- Dalam matematika ada namanya turunan ada juga namanya integral. Lalu, apa itu integral? Ia adalah lawan dari turunan atau diferensiasi. Sobat di Kelas XII pasti akan mendapatkan materi matematika ini. Integral juga dikenal sebagai antidiferensial dan dilambangkan dengan bentuk :
Sebuah fungsi F(X) disebut sebagai integral dari f(x) selagi apabila turunan pertama F'(x) = f(x). Jadi sebuah persamaan jika diturunkan kemudian diintegralkan akan mengahasilkan persamaan seperti bentuk awal.
Contoh Sobat punya persamaan f(x) = x2 + 2x, ketika persamaan itu di turunakan maka akan menghasilkan f'(x) = 2x + 2. Dengan menggunakan integral akan dapat mengembalikan bentuk 2x + 2 ke bentuk x2 + 2x. Jika turunan menurunkan 1 tingkat eksponen dari x2 ke x maka integral akan mengembalikan tingkat eksponen satu tingkat lebih tinggi, misal x menjadi x2, x2menjadi x3, dan seterusnya. Ada dua macam integral yaitu integral tak tentu dan integral tentu.
Integral Tak Tentu
Yang dinamakan integral tak tentu adalah integral yang tidak memiliki batas atas dan bawah. Biasanya hanya berupa integral dari sebuah aljabar matematika. Bentuk integral ini tidak memiliki daerah asal dan tidak memiliki daerah hasil
∫ f(x) dx = F(x) + c
Integral Tentu
Pondasi dasar tentang integral tentu pertama kali diperkenalkan oleh Newton dan Leibinz yang kemudian dieperkenalkan secara modern oleh Riemann. Integral ini memiliki batas atas dan batas bawah. Dalam aplikasinya, integral tentu banyak digunakan untuk menghitung luas di bawah kurva dengan batas tertentu atau menghitung volume benda jika diputar.
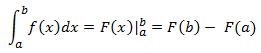
Mengenal Sifat dan Rumus Integral
berikut ini sifat-sifat dari operasi integral

Rumus Dasar Integral
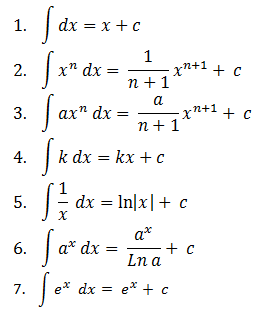
selain rumus dasar di atas, sobat bisa menggunakan rumus cepat lagi praktis
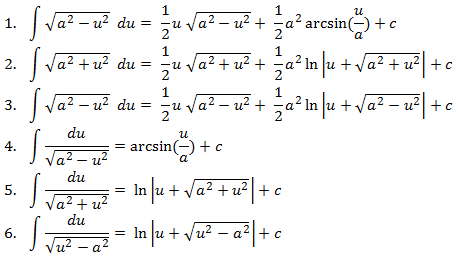
Integral Fungsi Aljabar
Jika ada fungsi aljabar yang diintegralkan maka sobat bisa menggunakan rumus berikut:

contoh, jika sobat punya aljabar 2x + 5 ketika diitegralkan akan mendapatkan hasil sebagai berikut:
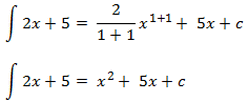
Integral Fungsi Eksponen
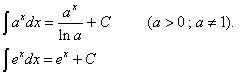
contoh:
∫ 3e4x dx Kita misalkan 4x = u sehingga persamaan di atas menjadi
∫ 3e4x dx = ∫ 3eu du/4
= 3/4 ∫ 3eu du
= 3/4 eu + c
= 3/4 e4x + C
Intgeral Fungsi Trigonometri
berikut rumus integral dari trigonometri yang sering dipakai dalam soal-soal matematika.
a. Integral dengan variabel sudut x atau sudut ax
∫ sin x dx = – cos x + c
∫ cos x dx = sin x + c
∫ sin ax dx = – (1/a) cos ax + c
∫ cos ax dx = (1/a) sin ax + c
∫ secs2 x dx = tan x + c
b. Integral dengan Bentuk Pangkat
Rumus Integral Matematika
Rumus Integral Matematika- Dalam matematika ada namanya turunan ada juga namanya integral. Lalu, apa itu integral? Ia adalah lawan dari turunan atau diferensiasi. Sobat di Kelas XII pasti akan mendapatkan materi matematika ini. Integral juga dikenal sebagai antidiferensial dan dilambangkan dengan bentuk :
Sebuah fungsi F(X) disebut sebagai integral dari f(x) selagi apabila turunan pertama F'(x) = f(x). Jadi sebuah persamaan jika diturunkan kemudian diintegralkan akan mengahasilkan persamaan seperti bentuk awal.
Contoh Sobat punya persamaan f(x) = x2 + 2x, ketika persamaan itu di turunakan maka akan menghasilkan f'(x) = 2x + 2. Dengan menggunakan integral akan dapat mengembalikan bentuk 2x + 2 ke bentuk x2 + 2x. Jika turunan menurunkan 1 tingkat eksponen dari x2 ke x maka integral akan mengembalikan tingkat eksponen satu tingkat lebih tinggi, misal x menjadi x2, x2menjadi x3, dan seterusnya. Ada dua macam integral yaitu integral tak tentu dan integral tentu.
Integral Tak Tentu
Yang dinamakan integral tak tentu adalah integral yang tidak memiliki batas atas dan bawah. Biasanya hanya berupa integral dari sebuah aljabar matematika. Bentuk integral ini tidak memiliki daerah asal dan tidak memiliki daerah hasil
∫ f(x) dx = F(x) + c
Integral Tentu
Pondasi dasar tentang integral tentu pertama kali diperkenalkan oleh Newton dan Leibinz yang kemudian dieperkenalkan secara modern oleh Riemann. Integral ini memiliki batas atas dan batas bawah. Dalam aplikasinya, integral tentu banyak digunakan untuk menghitung luas di bawah kurva dengan batas tertentu atau menghitung volume benda jika diputar.
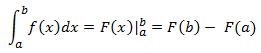
Mengenal Sifat dan Rumus Integral
berikut ini sifat-sifat dari operasi integral

Rumus Dasar Integral
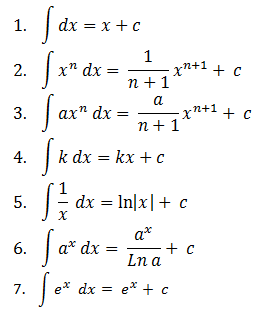
selain rumus dasar di atas, sobat bisa menggunakan rumus cepat lagi praktis
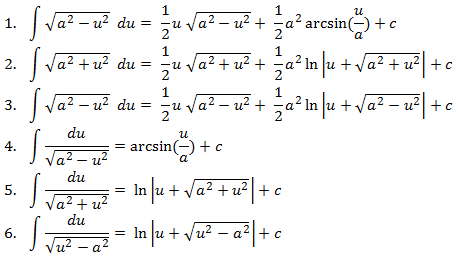
Integral Fungsi Aljabar
Jika ada fungsi aljabar yang diintegralkan maka sobat bisa menggunakan rumus berikut:

contoh, jika sobat punya aljabar 2x + 5 ketika diitegralkan akan mendapatkan hasil sebagai berikut:
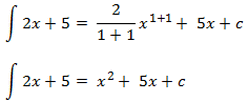
Integral Fungsi Eksponen
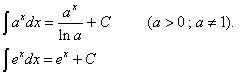
contoh:
∫ 3e4x dx Kita misalkan 4x = u sehingga persamaan di atas menjadi
∫ 3e4x dx = ∫ 3eu du/4
= 3/4 ∫ 3eu du
= 3/4 eu + c
= 3/4 e4x + C
Intgeral Fungsi Trigonometri
berikut rumus integral dari trigonometri yang sering dipakai dalam soal-soal matematika.
a. Integral dengan variabel sudut x atau sudut ax
∫ sin x dx = – cos x + c
∫ cos x dx = sin x + c
∫ sin ax dx = – (1/a) cos ax + c
∫ cos ax dx = (1/a) sin ax + c
∫ secs2 x dx = tan x + c
b. Integral dengan Bentuk Pangkat
∫sinn x. cos x dx = (1/(n+1)) sinn+1 x + c
∫ cosn x.sin x dx = (-1/(n+1)) cosn+1 + c
∫ sinn x dx = ∫ sinn-1 x. sin x dx (jika n ganjil)
∫ cosn x dx = ∫ cosn-1x . cos x dx (jika n ganjil)
∫ sinn x dx = ∫ (sin2 x)n/2 dx (jika n genap)
∫ cosn x dx = ∫ (cos2 x)n/2 dx (jika n genap)
baca juga rumus-rumus trigonometri
Metode-Metode Integral
Ada dua metode integral yang sering digunakan dalam menyelesaikan soal. Mereka adalah metode substitusei (penggantian) dan metode parsial. Berikut penjelasannya
a. Metode Substitusi
Untuk mengintegralkan sebuah alajabar sobat bisa menggunakan metode penggantian atau substitusi. Misalkan u = g(x) dengan g(x) merupkan fungsi yang mempunyai turunan maka
∫ f(g(x)).g'(x) = ∫ f(u).du = F(u) + c
biar lebih paham rumusnya yuk simak contoh soal berikut:

Kunci dari pemecahan soal di atas adalah permisalan 1/x kita misalkan dengan u. Jadi untuk memecahkan soal-soal integral dengan cara ini sobat harus pandai-pandai membuat permisalan. Berikut contoh lainnya:
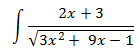
kita misalkan 3x2 + 9x -1 sebagai u
sehingga du = 6x + 9
2x + 3 = 1/3 (6x + 9) = 1/3 du

sekranga kita ganti kembali u dengan 3x2 + 9x -1 sehingga didapatkan jawaban:
b. Metode Parsial
Teknik atau metode lain yang bisa digunakan untuk melakukan integral adalah dengan metode parsial. Teknik ini biasanya digunakan untuk mencari suatu fungsi yang tidak dapat dicari integralnya jika menggunakan cara substitusi seperti pada huruf a di atas.
Jika u = f(x) dan v = g(x) maka berlaku rumus integral parsial:
∫ u.dv = u.v – ∫ v. du
Contoh Soal:
Berapa hasil dari ∫ x sin x ?
kita misalkan u = x maka du = dx
dv = sin x maka v = -cos x
(lihat rumus integral trigonometri sebelumnya)
kita masukkan ke rumus
∫ u.dv = u.v – ∫ v. du
∫ x sin x = x (-cos x) – ∫ (-cos x) dx = -x . cos x + sin x + c
Penggunaan Trigonometri Untuk Mencari Luas Daerah di Bawah Kurva dan Volume Benda Putar
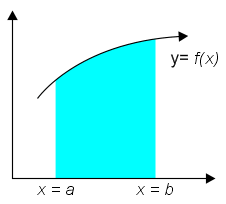
Salah satu penggunaan integral adalah untuk mencari luas daerahh di bawah 1 atau lebih kurva. Berikut kami rangkumkan ilustrasi gambar berikut rumusnya:
Luas daerah yang dibatasi kurva dan sumbu x
untuk mencari luas di bawah sebuah kurva sobat cukup mengintegralkan persamaan garis tersebut kemudian memasukkan nilai x.
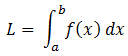
Luas Daerah yang Dibatasi Dua Kurva dan Sumbu X
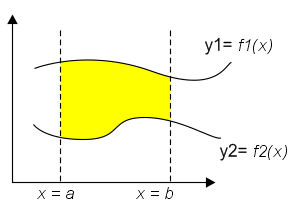
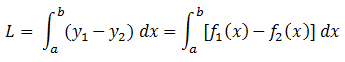
b. Volume Benda Putar
Selain bisa digunakan untuk menghitung luasan di bawah kurva, integral bisa juga digunakan untuk mencari volume benda putar. Volume benda putar adalah volume benda yang terjadi ketika sebuah bidang dua dimensi diputar menurut sumbu tertentu (x atau y).
Email This










